排列组合的一些公式及推导

绪论：加法原理、乘法原理

分类计数原理：做一件事，有 $n$ 类办法，在第 $1$ 类办法中有 $m_{1}$ 种不同的方法，在第 $2$ 类办法中有 $m_{2}$ 种不同的方法，…，在第 $n$ 类办法中有 $m_{n}$ 种不同的方法，那么完成这件事共有 $N = m_{1} + m_{2} + \dots + m_{n}$ 种不同的方法。

分步计数原理：完成一件事，需要分成 $n$ 个步骤，做第 $1$ 步有 $m_{1}$ 种不同的方法，做第 $2$ 步有 $m_{2}$ 种不同的方法，…，做第 $n$ 步有 $m_{n}$ 种不同的方法，那么完成这件事共有 $N = m_{1} \times m_{2} \times \dots \times m_{n}$ 种不同的方法。

区别：分类计数原理是加法原理，不同的类加起来就是我要得到的总数；分步计数原理是乘法原理，是同一事件分成若干步骤，每个步骤的方法数相乘才是总数。

排列数

从 $n$ 个不同元素种取出 $m$ （ $m \leq n$ ）个元素的所有不同排列的个数，叫做从 $n$ 个不同元素种取出 $m$ 个元素的排列数，用符号 $A_{n}^{m}$ 表示。

排列数公式

A_{n}^{m} = n (n - 1) (n - 2) \dots (n - m + 1) = \frac{n !}{( n - m )!}, n, m \in N, m \leq n

（规定 $0! = 1$ ）

推导：把 $n$ 个不同的元素任选 $m$ 个排序，按计数原理分步进行：

取第一个：有 $n$ 种取法；
取第二个：有 $(n - 1)$ 种取法；
取第三个：有 $(n - 2)$ 种取法；
……
取第 $m$ 个：有 $(n - m + 1)$ 种取法；

根据分步乘法原理，得出上述公式。

排列数性质

$A_{n}^{m} = n A_{n - 1}^{m - 1}$ 可理解为「某特定位置」先安排，再安排其余位置。

$A_{n}^{m} = m A_{n - 1}^{m - 1} + A_{n - 1}^{m}$ 可理解为：含特定元素的排列有 $m A_{n - 1}^{m - 1}$ ，不含特定元素的排列为 $A_{n - 1}^{m}$ 。

组合数

从 $n$ 个不同元素种取出 $m (m \leq n)$ 个元素的所有不同组合的个数，叫做从 $n$ 个不同元素种取出 $m$ 个元素的组合数，用符号 $C_{n}^{m}$ 表示。

组合数公式

C_{n}^{m} = \frac{A _{n}^{m}}{A _{m}^{m}} = \frac{n ( n - 1 ) ( n - 2 ) \dots ( n - m + 1 )}{m !} = \frac{n !}{m ! ( n - m )!}, n, m \in N, m \leq n

C_{n}^{0} = C_{n}^{n} = 1

证明：利用排列和组合之间的关系以及排列的公式来推导证明。

将部分排列问题 $A_{n}^{m}$ 分解为两个步骤：

第一步，就是从 $n$ 个球中抽 $m$ 个出来，先不排序，此即组合数问题 $C_{n}^{m}$ ；

第二步，则是把这 $m$ 个被抽出来的球排序，即全排列 $A_{m}^{m}$ 。

根据乘法原理， $A_{n}^{m} = C_{n}^{m} A_{m}^{m}$ ，那么

C_{n}^{m} = \frac{A _{n}^{m}}{A _{m}^{m}} = \frac{n ( n - 1 ) ( n - 2 ) \dots ( n - m + 1 )}{m !} = \frac{n !}{m ! ( n - m )!}

组合数的性质

$C_{n}^{m} = C_{n}^{n - m}$ 可以理解为：将原本的每个组合都反转，把原来没选的选上，原来选了的去掉，这样就变成从 $n$ 个元素种取出 $n - m$ 个元素，显然方案数是相等的。

递推公式 $C_{n}^{m} = C_{n - 1}^{m} + C_{n - 1}^{m - 1}$ 可理解为：含特定元素的组合有 $C_{n - 1}^{m - 1}$ ，不含特定元素的排列为 $C_{n - 1}^{m}$ 。还不懂？看下面。

Example

从 $1$ ，2，3，4，5（ $n = 5$ ）中取出 2（ $m = 2$ ）个元素的组合（ $C_{n}^{m}$ ）：

12 13 14 15 23 24 25 34 35 45

显然，这些组合中要么含有元素「1」，要么不含。

其中含有「1」的是：12 13 14 15
把里面的「1」都挖掉：2 3 4 5
而上面这个等价于从 2，3，4，5（ $n - 1$ ）中取出 1（ $m - 1$ ）个元素的组合。
其中不含「1」的是：23 24 25 34 35 45 上面等价于从 2，3，4，5（ $n - 1$ ）中取出 2（ $m$ ）个元素的组合。

而总方案数等于上面两种情况方案数之和，即 $C_{n}^{m} = C_{n - 1}^{m} + C_{n - 1}^{m - 1}$ 。

组合数求和公式

C_{n}^{0} + C_{n}^{1} + C_{n}^{2} + \dots + C_{n}^{n} = 2^{n}

我们感性认知一下，上面这个式子的左边表示什么呢？

把从 $n$ 个球中抽出 $0$ 个球的组合数（值为 $1$ ）、抽出 $1$ 个球的组合数、抽出 $2$ 个球的组合数、……、抽出 $n$ 个球的组合数相加。

换句话说，就是从 $n$ 个球中随便抽出一些不定个数球，问一共有多少种组合。

对于第 $1$ 个球，可以选，也可以不选，有 $2$ 种情况。
对于第 $2$ 个球，可以选，也可以不选，有 $2$ 种情况。
对于任意一个球，可以选，也可以不选，有 $2$ 种情况。

根据乘法原理，一共 $n 个 2 相乘 2 \times 2 \times \dots \times 2 = 2^{n}$ 种组合。

想要严谨的证明？数学归纳法：

当 $n = 1$ 时， $C_{1}^{0} + C_{1}^{1} = 2 = 2^{1}$ 成立。
假设 $n = k$ 时等式成立，即
$i = 0 \sum k C_{k}^{i} = 2^{n}$
成立，当 $n = k + 1$ 时，
$= = = = C_{k + 1}^{0} + C_{k + 1}^{1} + C_{k + 1}^{2} + \dots + C_{k + 1}^{k} + C_{k + 1}^{k + 1} C_{k + 1}^{0} + (C_{k}^{0} + C_{k}^{1}) + (C_{k}^{1} + C_{k}^{2}) + \dots + (C_{k}^{k - 1} + C_{k}^{k}) + C_{k + 1}^{k + 1} (C_{k}^{0} + C_{k}^{1} + C_{k}^{2} + \dots + C_{k}^{k}) + (C_{k}^{0} + C_{k}^{1} + C_{k}^{2} + \dots + C_{k}^{k}) 2 \times 2^{k} 2^{k + 1}$
等式也成立。
由 $1$ 、 $2$ 得，等式对 $n \in N^{*}$ 都成立。

也可偷懒地用二项式定理证明：

(a + b)^{n} = k = 0 \sum n C_{n}^{k} a^{n - k} b^{k}

令 $a = b = 1$ ，就得到了

i = 0 \sum n C_{n}^{i} = 2^{n}

类似的公式（由 $C_{n}^{m} = C_{n}^{n - m}$ 推导）：

C_{n}^{0} + C_{n}^{2} + C_{n}^{4} + \dots = C_{n}^{1} + C_{n}^{3} + C_{n}^{5} + \dots = 2^{n - 1}

杨辉三角

这个神奇的图形和组合数、二项式定理密切相关。（图片来自百度百科）

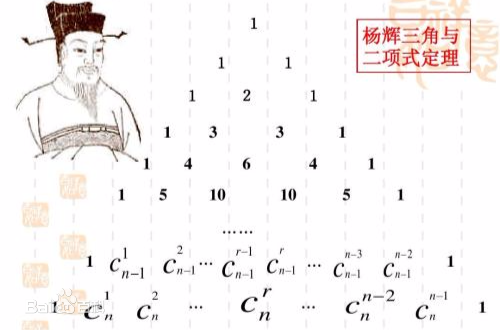
杨辉三角可以帮助你更好地理解和记忆组合数的性质：

第 $n$ 行的 $m$ 个数可表示为 $C_{n - 1}^{m - 1}$ ，即为从 $n - 1$ 个不同元素中取 $m - 1$ 个元素的组合数。
第 $n$ 行的数字有 $n$ 项。
每行数字左右对称（第 $n$ 行的第 $m$ 个数和第 $n - m + 1$ 个数相等， $C_{n}^{m} = C_{n}^{n - m}$ ），由 $1$ 开始逐渐变大。
每个数等于它上方两数之和（第 $n + 1$ 行的第 $i$ 个数等于第 $n$ 行的第 $i - 1$ 个数和第 $i$ 个数之和，即 $C_{n + 1}^{i} = C_{n}^{i} + C_{n}^{i - 1}$ ）。
$(a + b)^{n}$ 的展开式中的各项系数依次对应杨辉三角的第 $n + 1$ 行中的每一项（二项式定理）。

维基百科

以下来自维基百科（我只是随便贴这）

二项式系数

在数学上，二项式系数是二项式定理中各项的系数。一般而言，二项式系数由两个非负整数 $n$ 和 $k$ 为参数决定，写作 $(k n)$ ，定义为 $(1 + x)^{n}$ 的多项式展开式中， $x^{k}$ 项的系数，因此一定是非负整数。如果将二项式系数 $(0 n), (1 n), \dots, (n n)$ 写成一行，再依照 $n = 0, 1, 2, \dots$ 顺序由上往下排列，则构成帕斯卡三角形。

二项式系数常见于各数学领域中，尤其是组合数学。事实上，可以被理解为从 $n$ 个相异元素中取出 $k$ 个元素的方法数，所以大多读作「 $n$ 取 $k$ 」。二项式系数的定义可以推广至 $n$ 是复数的情况，而且仍然被称为二项式系数。

二项式系数亦有不同的符号表达方式，包括： $C (n, k)$ 、 $_{n} C_{k}$ 、 $^{n} C_{k}$ 、 $C_{n}^{k}$ 、 $C_{k}^{n}$ ，其中的 $C$ 代表组合（combinations）或选择（choices）。很多计算机使用含有 $C$ 的变种记号，使得算式只占一行的空间，相同理由也发生在置换数 $P_{k}^{n}$ ，例如写作 $P (n, k)$ 。

定义及概念

对于非负整数 $n$ 和 $k$ ，二项式系数 $(k n)$ 定义为 $(1 + x)^{n}$ 的多项式展开式中， $x^{k}$ 项的系数，即

(1 + x)^{n} = k = 0 \sum n (k n) x^{k} = (0 n) + (1 n) x + \dots + (n n) x^{n}

事实上，若 $x$ 、 $y$ 为交换环上的元素，则

(x + y)^{n} = k = 0 \sum n (k n) x^{n - k} y^{k}

此数的另一出处在组合数学，表达了从 $n$ 物中，不计较次序取 $k$ 物有多少方式，亦即从一 $n$ 元素集合中所能组成 $k$ 元素子集的数量。

有关二项式系数的恒等式

关系式

阶乘公式能联系相邻的二项式系数，例如在 $k$ 是正整数时，对任意 $n$ 有：

(k n + 1) = (k n) + (k - 1 n)

(k n) = \frac{n}{k} (k - 1 n - 1)

(k n - 1) - (k - 1 n - 1) = \frac{n - 2 k}{n} (k n)

两个组合数相乘可作变换：

(i n) (m i) = (m n) (i - m n - m)

一阶求和公式

r = 0 \sum n (r n) = 2^{n}

r = 0 \sum k (r n + r - 1) = (k n + k)

r = 0 \sum n - k \frac{( - 1 ) ^{r} ( n + 1 )}{k + r + 1} (r n - k) = (k n)^{- 1}

r = 0 \sum n (d r d n) = \frac{1}{d} r = 1 \sum d (1 + e^{\frac{2 π r i}{d}})^{d n}

i = m \sum n (i a + i) = (n a + n + 1) - (m - 1 a + m)

(m - 1 a + m) + (m a + m) + (m + 1 a + m + 1) + ... + (n a + n) = (n a + n + 1)

与斐波那契数列的关系

F_{n} = i = 0 \sum \infty (i ni)

F_{n - 1} + F_{n} = i = 0 \sum \infty (i n - 1 - i) + i = 0 \sum \infty (i n - i) = 1 + i = 1 \sum \infty (i - 1 n - i) + i = 1 \sum \infty (i n - i) = 1 + i = 1 \sum \infty (i n + 1 - i) = i = 0 \sum \infty (i n + 1 - i) = F_{n + 1}

主条目：朱世杰恒等式

i = m \sum n (a i) = (a + 1 n + 1) - (a + 1 m)

(a + 1 m) + (a m) + (a m + 1) ... + (a n) = (a + 1 n + 1)

二阶求和公式

r = 0 \sum n (r n)^{2} = (n 2 n)

i = 0 \sum n (r _{1} - 1 r _{1} + n - 1 - i) (r _{2} - 1 r _{2} + i - 1) = (r _{1} + r _{2} - 1 r _{1} + r _{2} + n - 1)

生成函数方法

(1 - x)^{- r_{1}} (1 - x)^{- r_{2}} = (1 - x)^{- r_{1} - r_{2}}

(1 - x)^{- r_{1}} (1 - x)^{- r_{2}} = (n = 0 \sum \infty (r _{1} - 1 r _{1} + n - 1) x^{n}) (n = 0 \sum \infty (r _{2} - 1 r _{2} + n - 1) x^{n}) = n = 0 \sum \infty (i = 0 \sum n (r _{1} - 1 r _{1} + n - 1 - i) (r _{2} - 1 r _{2} + i - 1)) x^{n}

(1 - x)^{- r_{1} - r_{2}} = n = 0 \sum \infty (r _{1} + r _{2} - 1 r _{1} + r _{2} + n - 1) x^{n}

主条目：范德蒙恒等式

i = 0 \sum k (i n) (k - i m) = (k n + m)

三阶求和公式

主条目：李善兰恒等式

(k n + k)^{2} = j = 0 \sum k (j k)^{2} (2 k n + 2 k - j)

排列组合的一些公式及推导 ​

绪论：加法原理、乘法原理 ​

排列数 ​

排列数公式 ​

排列数性质 ​

组合数 ​

组合数公式 ​

组合数的性质 ​

组合数求和公式 ​

杨辉三角 ​

维基百科 ​

定义及概念 ​

有关二项式系数的恒等式 ​

关系式 ​

一阶求和公式 ​

二阶求和公式 ​

三阶求和公式 ​