圆锥曲线与极坐标 参考 https://zhuanlan.zhihu.com/p/33808071
极坐标 在平面内取一个定点 O O x M ρ OM r θ O x OM ρ M θ M ( ρ , θ ) M
极坐标系用长度和角度取代了二维的坐标,相对于一般的直角坐标为下面的优点:
设 M ( x , y ) ( ρ , θ ) 互化公式 :
{ x y = ρ cos θ = ρ sin θ or { ρ 2 tan θ = x 2 + y 2 = x y ( x = 0 )
圆锥曲线的极坐标方程 (1)以焦点为极点
记 ∣ PF ∣ = ρ P l d p d ρ = e d = p + ρ cos θ p + ρ c o s θ ρ = e 圆锥曲线的统一极坐标方程 :
ρ = 1 − e cos θ e p
当 e = 0 0 < e < 1 e = 1 e > 1
(2)以坐标原点为极点
在这里只考虑椭圆与双曲线的情况,抛物线也可类比:
椭圆或双曲线的标准方程(焦点在 x a 2 x 2 ± b 2 y 2 = 1
代入 x = ρ cos θ y = ρ sin θ
a 2 ρ 2 c o s 2 θ ± b 2 ρ 2 s i n 2 θ = 1 ρ 2
ρ 2 1 = a 2 cos 2 θ ± b 2 sin 2 θ 此方程表示椭圆或双曲线的轨迹。
取加号时,轨迹为椭圆;取减号时,轨迹为双曲线。
一些结论
如图,F 圆锥曲线 E F E A , B A B α
∣ A F ∣ = 1 − e cos α e p , ∣ BF ∣ = 1 + e cos α e p ∣ A B ∣ = 1 − e c o s α e p + 1 + e c o s α e p = 1 − e 2 cos 2 α 2 e p
(看成以 F ρ = 1 − e c o s θ e p θ = α A ρ ∣ A F ∣ θ = α + π B cos ( θ + π ) = − cos θ
当椭圆与双曲线以标准方程表示时,焦准距 p = c b 2 e = a c
∣ A F ∣ = a − c cos α b 2 , ∣ BF ∣ = a + c cos α b 2 ∣ A B ∣ = a 2 − c 2 cos 2 α 2 a b 2
若 ∣ BF ∣ ∣ A F ∣ = λ 1 − e c o s α 1 + e c o s α = λ
e cos α = λ + 1 λ − 1
已知 e , λ
特殊地,当该曲线为抛物线时,e = 1
∣ A F ∣ = 1 − cos α p ∣ BF ∣ = 1 + cos α p ∣ A B ∣ = sin 2 α 2 p
应用 (1)以焦点为极点
例 1 (2017 年全国Ⅰ卷)10.已知 F C : y 2 = 4 x l 1 l 2 l 1 C A B l 2 C D E ∣ A B ∣ + ∣ D E ∣
解 p = 2 A B α D E α + 2 π
使用结论:∣ A B ∣ = s i n 2 α 2 p = s i n 2 α 4 ∣ D E ∣ = s i n 2 ( α + 2 π ) 4 = c o s 2 α 4
所以 ∣ A B ∣ + ∣ D E ∣ = s i n 2 α 4 + c o s 2 α 4 = ( s i n 2 α 4 + c o s 2 α 4 ) × 1 = ( s i n 2 α 4 + c o s 2 α 4 ) ( sin 2 α + cos 2 α ) ≥ ( s i n α 2 sin α + c o s α 2 cos α ) 2 = ( 2 + 2 ) 2 = 16
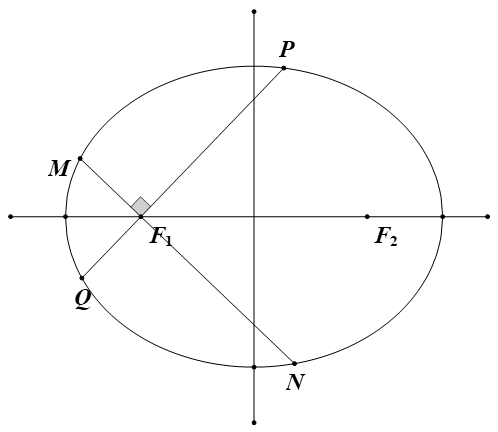
例 2 (模型来自于同济大学自招题)已知椭圆 C : 4 x 2 + 3 y 2 = 1 M , N , P , Q MNPQ
解 依题意 e = 2 1 p = 3 PQ α MN α + 2 π
∣ PQ ∣ = 1 − e 2 c o s 2 α 2 e p = 4 − c o s 2 α 12 = s i n 2 α + 3 12
用 α + 2 π α ∣ MN ∣ = c o s 2 α + 3 12
所以 S = 2 1 ∣ PQ ∣∣ MN ∣ = ( 4 − c o s 2 α ) ( c o s 2 α + 3 ) 72
此处换元后易求得范围。
例 3 已知梯形 A BC D A B / / C D ∠ B A D = 4 5 ∘ A D Γ B , C C D = 7 A B Γ 4 3 2 2 2 3 2 2 2
解 延长 C D Γ E D E = A B D E C D = A B C D = 7 λ = 7
运用结论 e cos 4 5 ∘ = λ + 1 λ − 1 2 e = 8 6 = 4 3 e = 4 3 2
(2)以坐标原点为极点
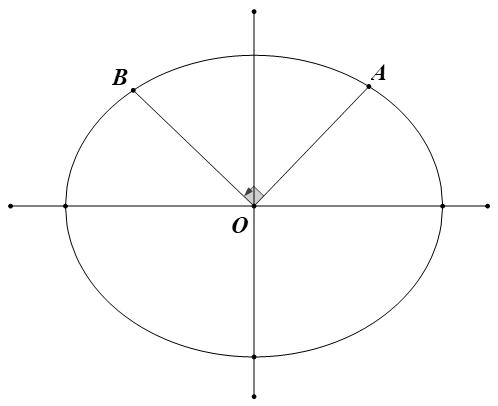
例 4 已知椭圆 C : a 2 x 2 + b 2 y 2 = 1 O A OB A , B O A ⊥ OB ∣ O A ∣ 2 1 + ∣ OB ∣ 2 1
解 1 以坐标原点为极点,x
x = ρ cos θ y = ρ sin θ
ρ 2 1 = a 2 c o s 2 θ + b 2 s i n 2 θ
设直线 O A θ OB θ + 2 π
∣ O A ∣ 2 1 = ρ 1 2 1 = a 2 c o s 2 θ + b 2 s i n 2 θ
用 θ + 2 π θ
∣ OB ∣ 2 1 = ρ 2 2 1 = a 2 s i n 2 θ + b 2 c o s 2 θ
两式相加得: ∣ O A ∣ 2 1 + ∣ OB ∣ 2 1 = a 2 c o s 2 θ + s i n 2 θ + b 2 s i n 2 θ + c o s 2 θ = a 2 1 + b 2 1
用此方法的证明极度简洁,但担心会被扣分,因此给出如下“角参”的做法:
解 2 记 ∣ O A ∣ = m ∣ OB ∣ = n ∠ A O x = θ ∠ BO x = θ + 2 π
则 A ( m cos θ , m sin θ ) B ( n cos ( θ + 2 π ) , n sin ( θ + 2 π )) B ( − n sin θ , n cos θ )
m 2 1 = a 2 c o s 2 θ + b 2 s i n 2 θ
n 2 1 = a 2 s i n 2 θ + b 2 c o s 2 θ
两式相加得: m 2 1 + n 2 1 = a 2 c o s 2 θ + s i n 2 θ + b 2 s i n 2 θ + c o s 2 θ = a 2 1 + b 2 1
其实本质上还是极坐标的思想,不过这样写就不会被当作超纲了。
在这里有人可能会想到椭圆的参数方程: ( a cos θ , b sin θ ) θ